Settlers of Catan Grids

Settlers of Catan is a popular board game with many expansions centering around the development of competing settlements on an island made of tiles arranged in a hexagonal grid... or is it?

Well of course the intent and aesthetic of the game portrays the game board as a hexagonal grid, I would not argue otherwise, but is the best model for understanding the placement of game pieces in Catan really a hexagonal grid? I would disagree. First let's look at a typical Settlers of Catan game board (all the expansions do not differ enough in terms of board layout, rules, and behavior to consider them all seperately).

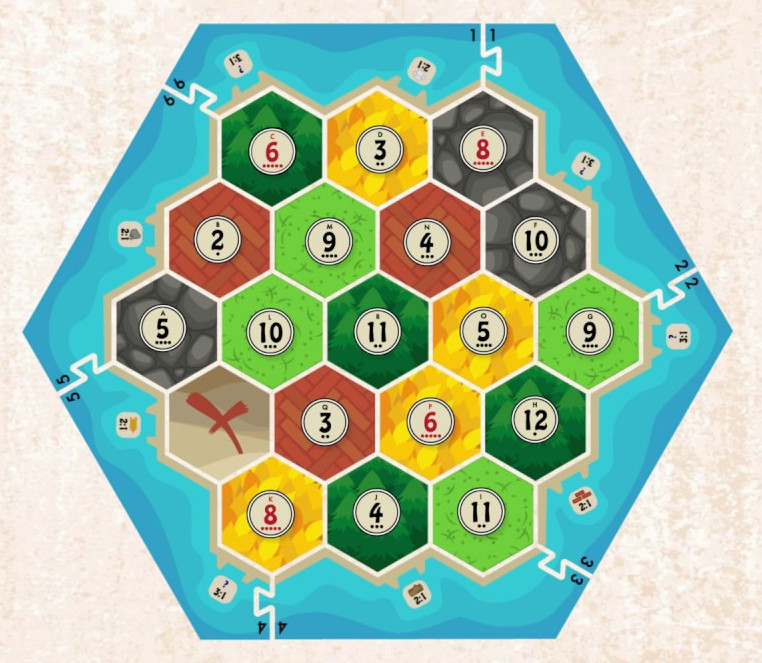
Lets break down the information the board contains:

• Tile types
• Tile numbers
• Edges for road/ship placement
• Vertices for settlement and city placement and ports

Every hexagonal tile on the board has one of five resources (excluding expansions):

• Forest (Lumber Resource)
• Pasture (Wool Resource)
• Fields (Grain Resource)
• Hills/River (Brick Resource)
• Mountains (Ore Resource)
• Desert
• Ocean

However the game is centered around player-placed settlements and roads, which in this default model means that roads occupy the edges and the settlements occupy the vertices. The model is resource-centric rather than centering around settlements and roads. In addition I personally dislike hexagonal coordinate systems (there are a variety) and the overcomplicated process of dealing with finding the longest path formed by edges on a hexagonal grid between its vertices (rather than faces). The coordinate systems for dealing with the edges of hexagons versus their faces or vertices are particularly atrocious.

(credit to red blob games)

Instead, because the overall board itself is always in the shape of a hexagon, we can use a simple trick to make these problems far easier to understand while simultaneously modeling the board around settlements and roads instead of resources. It is pretty simple but I am going to review some mathematics terminology involved to understand how it works.

Dualization, a Mirror Way of Looking At Mathematical Objects

In Mathematics the term "Dual" can have a variety of meanings. In the context of graph theory every graph has a dual graph which is created by forming a vertex from every face of the original graph and forming the edges of the dual graph by connecting edges between these new vertices whenever they are bisected by an edge of the old graph. A famous example of a dual pair of graphs which you may be familiar with (at least half of at least) would be Voronoi diagrams and their corresponding Delaunay triangulations which are formed by dualizing the Voronoi diagram. Or the Delaunay triangulations can be used to form Voronoi diagrams, the function to find a dual graph is an involutory function, where f(f(x))=x, so it works both ways.

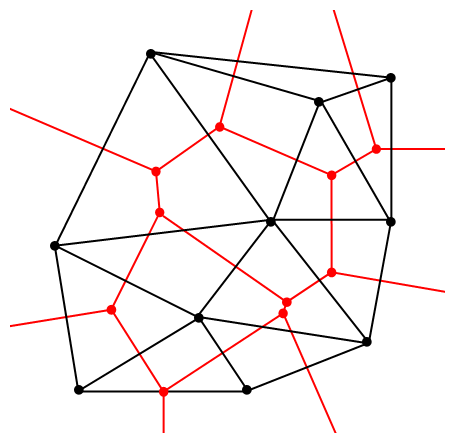
This can be used on grids as well! We can take the dual of the default hexagonal grid which is traditionally used to model the Settlers of Catan game board to get a hexagonally-shaped triangle grid where the new faces of the grid represent all of the possible settlement locations and their three accessible resources.

Modeling a Dualized Catan

So now the faces of the hexagons are vertices (as well as all the previous vertices in the grid) and each hexagon has been transformed into six triangles. Each triangle face in the grid contains only one settlement location, so we can take these triangles to represent settlements themselves. This has the additional benefit of allowing for the use of a more traditional 2-dimensional cartesian coordinate system where each coordinate represents a settlement location and only needs two dimensions rather than three. In addition were the board hexagonal and the tiles used as the main unit of infomation on the board there would be the question of which tile each settlement belongs to (duplicating data between hexes would make consistency between changed states of the game difficult since the same data would be updated two or three times), which is no longer a problem when using these "Tris". This is illustrated below.

But how do the other elements of Catan represented on the original game board translate to this new model based on the dual of the game board? We also need to have ways of storing roads, resource information, and die roll numbers. Answering the roads question is fairly straightforward. Roads are represented by the edges between two triangles in the grid. So a road would be the edge shared by Tri (0,0) and Tri (0,1) for example. The fact that they are perpendicular to the road orientation on a typical board is not significant except for aesthetics. Being able to quickly and easily describe where the road is on the board is more significant mathematically.

What is not as clear is how we should represent resource tiles and their roll numbers. This is a problem similair to the problem in the original hexagonal grid about which hex is where settlement or road belongs to be stored as data. The difference now is that unlike settlements and roads, it does not matter as much if there is duplicate data between Tris storing a resource type and roll number. Each Tri can simply store the roll number and type of the three surrounding resources.

Notice that I said as much in the above paragraph. The only problem that comes into play would be keeping track of the robber location and which resources in each Tri are inaccessible due to robber placement at any given time. I would argue that this issue is a fairly trivial drawback, however, compared to the advantages of modeling the board with the dualized grid. The elimination of complexity in the problem of identifying longest-road (one of the victory conditions in Settlers of Catan) as well as the de-duplication and organization of settlement and road data is enough to compensate in terms of effort.

Hopefully from this you have learned something about grids, mathematical duals, and problem solving when modeling a system that appears straightforward to humans but maybe is not so mathematically clear or easily understood by a computer (but the road is right there!). Otherwise I hope it was at least a little bit interesting.